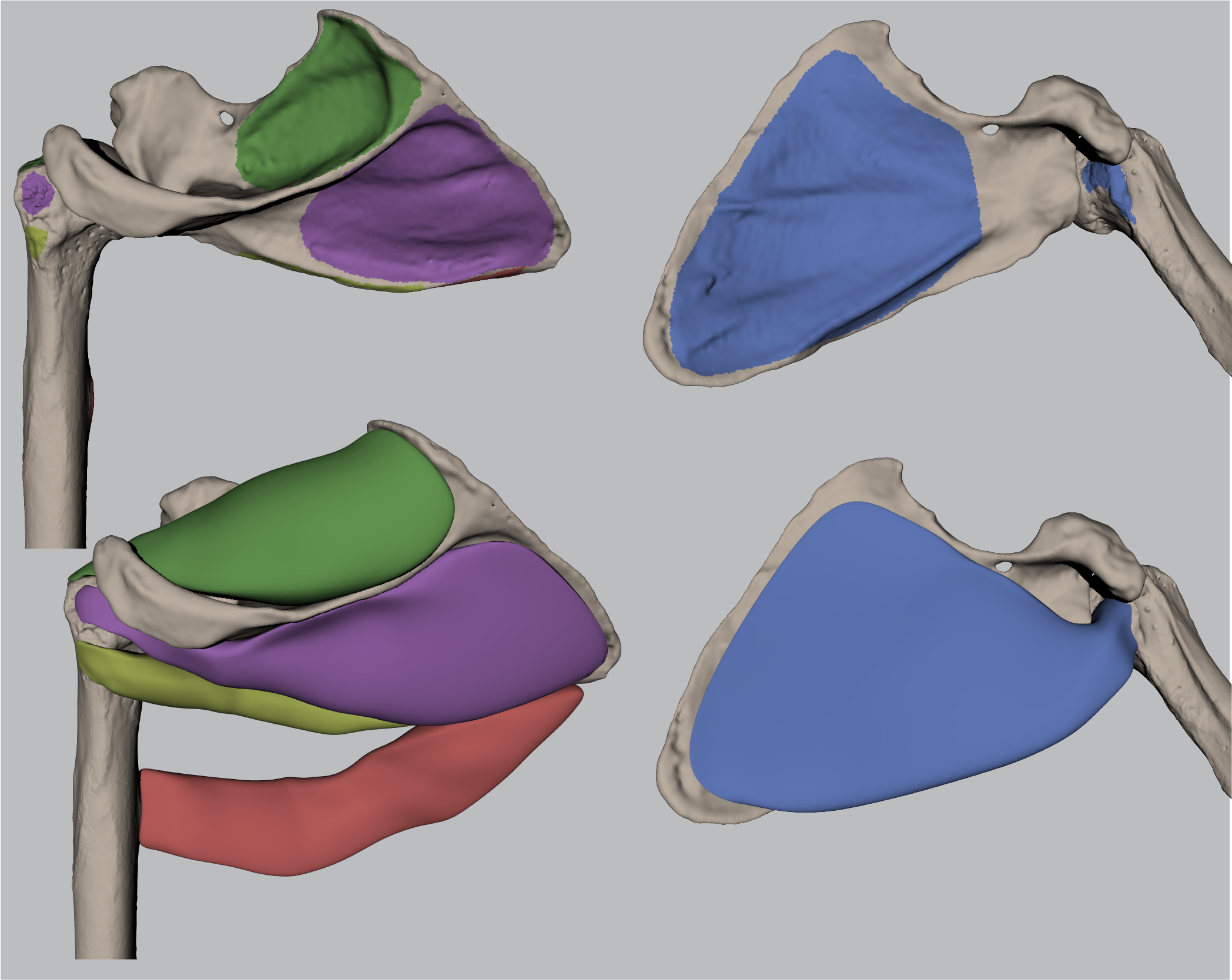
2. Results 3.3 Correlation Analysis of Supraspinatus, Infraspinatus and Subscapularis#
This Python script performs an analysis to determine the correlation between the log-transformed origin areas and volumes of specific shoulder muscles. The analysis is conducted for the following muscles:
Supraspinatus
Infraspinatus
Subscapularis
The log-transformation is applied to the origin areas and volumes to normalize the data and improve the accuracy of the correlation analysis.
2.1. Imports#
Required packages for this analysis can be found in the requirements.txt file. Ensure that all dependencies are installed before running the script.
Show code cell source
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np
import os
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
# ANSI escape code for bold text in print
bold_start = "\033[1m"
bold_end = "\033[0m"
2.2. Input Setup#
Loads the Muscle_data.xlsx file containing all original data and log transforms origin area and experimental volume.
Show code cell source
# Construct the relative path to the data file
file_path = os.path.join('Muscle_data.xlsx')
# Load the data from the Excel file
data = pd.read_excel(file_path)
# Apply logarithmic transformation to the Origin_Area and Muscle_Volume_rec
data['Log_Origin_Area'] = np.log(data['Origin_Area (cm²)'])
data['Log_Volume_exp'] = np.log(data['Volume_exp (cm³)'])
2.3. Filter data#
Remove Teres Major and Minor from the analysis to investigate them separately.
Show code cell source
# Filter out the rows where Muscle_Name is either 'Teres Major' or 'Teres Minor'
filtered_data = data[~data['Muscle_Name'].isin(['Teres Major', 'Teres Minor'])]# Filter out the rows where Muscle_Name is 'Teres Major'
# store transformed variables
muscle_origin = filtered_data['Log_Origin_Area']
muscle_volume = filtered_data['Log_Volume_exp']
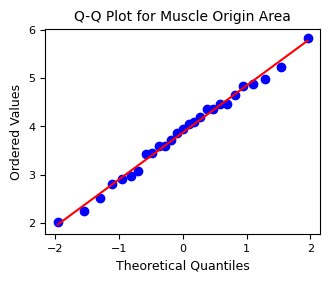
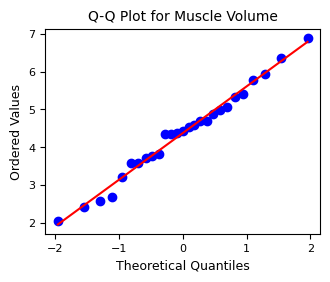
2.4. Tests for normality#
Performs a Shapiro-Wilk test and evaluates normality using Q-Q plots
Show code cell source
# Shapiro-Wilk test for normality
shapiro_test1 = stats.shapiro(muscle_origin)
shapiro_test2 = stats.shapiro(muscle_volume)
print("Shapiro-Wilk test for muscle origin: ", shapiro_test1)
print("Shapiro-Wilk test for muscle volume: ", shapiro_test2)
# Set figure size (convert cm to inches)
width_cm = 9
height_cm = width_cm * 0.75 # Aspect ratio of 4:3 (optional)
width_in = width_cm / 2.54
height_in = height_cm / 2.54
# Q-Q plot for data1
# Create figure with specified size
plt.figure(figsize=(width_in, height_in))
stats.probplot(muscle_origin, dist="norm", plot=plt)
plt.title("Q-Q Plot for Muscle Origin Area", fontsize=10)
plt.xlabel("Theoretical Quantiles", fontsize=9) # Set xlabel font
plt.ylabel("Ordered Values", fontsize=9) # Set ylabel font
# Apply custom font to tick labels
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
# Show Figure
plt.show()
# Q-Q plot for data2
plt.figure(figsize=(width_in, height_in))
stats.probplot(muscle_volume, dist="norm", plot=plt)
plt.title("Q-Q Plot for Muscle Volume", fontsize=10)
plt.xlabel("Theoretical Quantiles", fontsize=9) # Set xlabel font
plt.ylabel("Ordered Values", fontsize=9) # Set ylabel font
# Apply custom font to tick labels
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.show()
Shapiro-Wilk test for muscle origin: ShapiroResult(statistic=0.9892005715167651, pvalue=0.9907832024086947)
Shapiro-Wilk test for muscle volume: ShapiroResult(statistic=0.9838490399269613, pvalue=0.9369937392036665)
2.5. Pearson Correlation Analysis#
Show code cell source
# Correlation analysis
r, p = stats.pearsonr(muscle_origin, muscle_volume)
# Calculate degrees of freedom
n = len(muscle_origin)
df = n - 2
# Calculate confidence interval for Pearson correlation coefficient
alpha = 0.05 # significance level for 95% confidence interval
z = np.arctanh(r)
SE_z = 1 / np.sqrt(n - 3)
z_critical = stats.norm.ppf(1 - alpha / 2)
z_lower = z - z_critical * SE_z
z_upper = z + z_critical * SE_z
r_lower = np.tanh(z_lower)
r_upper = np.tanh(z_upper)
# Create p_tex value
if p < 0.001:
p_tex = "<0.001"
elif p < 0.05:
p_tex = "<0.05"
else:
p_tex = ">0.05"
# Calculate the linear regression
x = filtered_data['Log_Origin_Area']
y = filtered_data['Log_Volume_exp']
X = sm.add_constant(x) # add column for intercept
re = sm.OLS(y, X).fit()
# print the summary of the linear regression
print(re.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Log_Volume_exp R-squared: 0.911
Model: OLS Adj. R-squared: 0.907
Method: Least Squares F-statistic: 254.6
Date: Wed, 06 Nov 2024 Prob (F-statistic): 1.29e-14
Time: 16:29:16 Log-Likelihood: -9.9869
No. Observations: 27 AIC: 23.97
Df Residuals: 25 BIC: 26.57
Df Model: 1
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
const -0.3170 0.302 -1.049 0.304 -0.939 0.305
Log_Origin_Area 1.2119 0.076 15.957 0.000 1.056 1.368
==============================================================================
Omnibus: 0.619 Durbin-Watson: 1.327
Prob(Omnibus): 0.734 Jarque-Bera (JB): 0.691
Skew: 0.186 Prob(JB): 0.708
Kurtosis: 2.311 Cond. No. 18.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Show code cell source
# determine results
# determine prediction intervals boundaries
prstd, iv_l, iv_u = wls_prediction_std(re)
# determine slope and intercept
intercept = re.params.iloc[0] # The first parameter is the intercept
slope = re.params.iloc[1] # The remaining parameter is the slope
# determine y values for linear model
y_pred = slope * x + intercept
# Format the regression line equation
if intercept < 0:
regression_eq = f'y = {slope:.2f}x - {abs(intercept):.2f}'
else:
regression_eq = f'y = {slope:.2f}x + {intercept:.2f}'
# Reporting
print(f"\nThe Pearson correlation coefficient was found to be {bold_start}r = {r:.2f}{bold_end}, p = {p:.2e}, \nwith degrees of freedom df = {df} (n = {n}).\n")
print(f"95% Confidence interval for r: ({r_lower:.2f}, {r_upper:.2f})\n")
print(f"The Regression line equation is: {bold_start}{regression_eq}{bold_end}.\n")
# Figure settings Correlation
# Define the custom colors for each muscle
custom_colors = {
'Supraspinatus': (0.467, 0.710, 0.367),
'Infraspinatus': (0.7, 0.47, 0.82),
'Subscapularis': (0.45, 0.56, 0.87),
'Teres Minor': (0.741, 0.8, 0.384),
'Teres Major': (0.871, 0.435, 0.427)
}
# Define unique markers for Genus
custom_markers = {
'Hylobates': 'P',
'Symphalangus': 'X',
'Pongo': 'D',
'Gorilla': '^',
'Pan': 'v',
'Homo': 's'
}
# Set figure size (convert cm to inches)
width_cm = 17.7
height_cm = 10
width_in = width_cm / 2.54
height_in = height_cm / 2.54
# Create the figure and subplots
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(width_in, height_in), sharey=True)
# Scatter Plot all (left subplot)
ax1 = axes[0]
# Get unique muscle names and specimen names
muscle_names = data['Muscle_Name']
specimen_names = data['Genus']
# Plot each data point with the respective color and marker
for muscle, color in custom_colors.items():
for specimen, marker in custom_markers.items():
mask = (muscle_names == muscle) & (specimen_names == specimen)
sns.scatterplot(x='Log_Origin_Area', y='Log_Volume_exp', ax=ax1, data=data[mask],
color=color, marker=marker)
ax1.set_title('Origin Area and Volume of all Muscles', fontsize=10)
ax1.set_xlabel('Log Muscle Origin Area (cm$^2$)', fontsize=9)
ax1.set_ylabel('Log Muscle Volume (cm$^3$)', fontsize=9)
ax1.tick_params(axis='both', which='major', labelsize=8)
for label in (ax1.get_xticklabels() + ax1.get_yticklabels()):
label.set_size(8)
# Add annotation "a"
ax1.annotate('(a)', xy=(-0.1, 1.05), xycoords='axes fraction', fontsize=12)
# Correlation Supra, infra, subscap (right subplot)
ax2 = axes[1]
# Get unique muscle names and specimen names
muscle_names = filtered_data['Muscle_Name']
specimen_names = filtered_data['Genus']
# sort values before using the fill_between function
# Sort the values based on x (Log_Origin_Area)
sorted_indices = x.argsort()
x_sorted = x.iloc[sorted_indices]
iv_l_sorted = iv_l.iloc[sorted_indices]
iv_u_sorted = iv_u.iloc[sorted_indices]
# Plot the prediction intervals as shaded areas
ax2.fill_between(x_sorted, iv_l_sorted, iv_u_sorted, alpha=0.1, color='red', linewidth = 0) # 95% Prediction Interval
# Determine line for isometric scaling
Y = filtered_data['Log_Origin_Area'] + slope*min(filtered_data['Log_Origin_Area']) + intercept -min(filtered_data['Log_Origin_Area'])
ax2.plot(filtered_data['Log_Origin_Area'], Y, color='grey')
# Plot each data point with the respective color and marker
for muscle, color in custom_colors.items():
for specimen, marker in custom_markers.items():
mask = (muscle_names == muscle) & (specimen_names == specimen)
sns.scatterplot(x='Log_Origin_Area', y='Log_Volume_exp', ax=ax2, data=filtered_data[mask],
color=color, marker=marker)
# Plot regression line
sns.lineplot(x=x, y=y_pred, color='red', ax=ax2)
# Apply custom fonts to the plot
ax2.set_title('Supra- and Infraspinatus and Subscapularis',fontsize=10)
ax2.set_xlabel('Log Muscle Origin Area (cm$^2$)', fontsize=9)
ax2.set_ylabel('Log Muscle Volume (cm$^3$)', fontsize=9)
ax2.tick_params(axis='both', which='major', labelsize=8)
for label in (ax2.get_xticklabels() + ax2.get_yticklabels()):
label.set_size(8)
# Add annotation text
ax2.annotate(
f'Regression line: {regression_eq}\nPearson r: {r:.2f}\n95% CI: ({r_lower:.2f}, {r_upper:.2f})\np-value: {p_tex}',
xy=(0.05, 0.95), xycoords='axes fraction', fontsize=9,
horizontalalignment='left', verticalalignment='top'
)
# Add annotation "b"
ax2.annotate('(b)', xy=(-0.1, 1.05), xycoords='axes fraction', fontsize=12)
# Create custom legend handles
handles_muscles = [plt.Line2D([0], [0], marker='o', color='w', label=muscle,
markerfacecolor=color, markersize=10)
for muscle, color in custom_colors.items()]
# Create handles with italicized labels
handles_specimen = [
plt.Line2D(
[0], [0],
marker=marker,
color='w',
label=f'${specimen}$', # Italicize the label here
markerfacecolor='gray',
markersize=10
)
for specimen, marker in custom_markers.items()
]
# Add legends above and below the plots
fig.legend(handles=handles_specimen, title='Genus', loc='upper center', ncol=6)
fig.legend(handles=handles_muscles, title='Muscles', loc='lower center', ncol=6)
# Adjust layout to make room for legends
plt.tight_layout(rect=[0, 0.1, 1, 0.9]) # Leave space for legends
plt.show()
The Pearson correlation coefficient was found to be r = 0.95, p = 1.29e-14,
with degrees of freedom df = 25 (n = 27).
95% Confidence interval for r: (0.90, 0.98)
The Regression line equation is: y = 1.21x - 0.32.

Fig. 2.1 Manuscript Figure 4: Analysis of the correlation between muscle volume and origin area. (a) Scatter plot illustrating muscle volumes versus muscle origin areas for all muscles. (b) Pearson correlation of log-transformed data for the muscle origin areas and volumes of the supraspinatus, infraspinatus, and subscapularis muscles. The red line shows the best-fit linear regression between muscle origin area and volume. The red shaded area around the red line indicates the prediction intervals. The grey line represents the prediction assuming isometric scaling with a slope of one.#